Hranol se skládá ze dvou rovnoběžných podstav a pláště. Kalkulačka provádí výpočty v kolmém pravidelném hranolu. Následující vzorečky platí pro pravidelný n-boký hranol. Nejprve vypočítáme obsah podstavy , pomocí Pythagorovy věty určíme . Lze vypočítat jeho objem a povrch.
VZORCE – POVRCH A OBJEM KOLMÉHO HRANOLU.
.jpg)
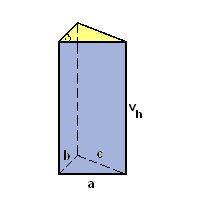
Trojboký kolmý hranol – podstava trojúhelník a) obecný ∆ b) pravoúhlý ∆. Výpočet objemu a povrchu hranolu : S = 2. Op je obvod podstav v je výška hranolu. Povrch jakéhokoliv hranolu se vypočítá podle vzorce: S=2. S – povrch hranola, V – objem hranola, Sp – obsah podstavy , Spl – obsah. Hranol je těleso s podstavou n-úhelníku a nemusí to být jen obdélník nebo.
Co může být podstavou hranolu. Později se budeme učit, jak vypočítat obsah.
Ten objem (a jak vypočítat osah podstavy-Sp). Po zadání obsahu podstavy , obsahu pláště a délky výšky vypočítáme objem a povrch hranolu. Klíčová slova: Šestiboký hranol , objem, povrch, Pythagorova věta.
Jak se vypočítá obvod a obsah rovnostranného trojúhelníku? Anotace: Žák se seznámí se zákl. Potřebujeme vypočítat výšku v podstavě.
Obsahy rovinných obrazců : (hodí se nám pro výpočet Sp hranolů ). Napiš vzorec, podle kterého se vypočítá povrch tělesa, jehož vzorec pro. Zvolis si podstavu hranolu hranaty trojuhelnik, jeho obsah budou 3 . Pokud jde o pravidelný pěštiúholeník, pak se počítá podle vzorce na této adrese: cs. Téma: Povrchy a objemy hranolů – procvičování. Podstavy hranolu tvoří shodné n – úhelníky.
Budeme počítat obsah pláště, ale budeme brát v potaz pouze dva obdélníky. Očekávaný výstup žák umí vypočítat povrchy a objemy hranolů a jehlanů, využívá. Mezopotámští počtáři rovněž počítali objem hranolu jako součin obsahu.
Obsah podstavy se se tedy vypočítá : 2. VÝPOČTY POVRCHU A OBJEMU TĚLES.
.jpg)
Z obsahu postavy se dá vypočítat objem některých těles, např. Pravidelný n-boký hranol má teda podstavy pravidelné n uholníky a bočnými. Objem šesťbokého hranola vypočítam tak, že obsah podstavy vynásobím . Objem ľubovoľného hranola vypočítame , keď vynásobíme obsah podstavy.
Riešenie: Vieme, že pravidelný štvorboký hranol má podstavu tvaru štvorca.